Mengungkap Keajaiban di Balik Suara: Peranan Krusial Matematika dalam Pemrosesan Suara

Pernahkah kamu bertanya-tanya bagaimana suara, sesuatu yang tak terlihat, bisa direkam, disimpan dalam perangkat digital, bahkan dimanipulasi menjadi berbagai efek? Rahasianya terletak pada keajaiban tersembunyi di balik gelombang suara: matematika. Ya, di balik alunan musik yang menyentuh hati, hiruk pikuk kota yang ramai, hingga bisikan angin yang menenangkan, terdapat persamaan dan algoritma yang bekerja dengan presisi tinggi.

Artikel ini akan mengajak kamu menyelami dunia menakjubkan pemrosesan suara dan mengungkap peran krusial matematika di dalamnya. Siapkan dirimu untuk menelusuri transformasi Fourier, filter digital, dan konsep-konsep matematika lainnya yang menjadi kunci di balik teknologi yang setiap hari kita nikmati. Dari rekaman musik hingga asisten virtual, mari kita bongkar misteri di balik keajaiban suara!

Menyelami Dasar Pemrosesan Suara

Di era digital yang serba canggih ini, teknologi berkembang dengan pesat, membuka pintu menuju berbagai kemungkinan baru. Salah satu terobosan paling menarik adalah bidang pemrosesan suara, yang merevolusi cara kita berinteraksi dengan mesin dan dunia di sekitar kita.

Secara sederhana, pemrosesan suara adalah bidang multidisiplin yang berkaitan dengan representasi digital sinyal audio dan teknik pemrosesannya. Ini adalah bidang yang luas yang mencakup berbagai aplikasi, mulai dari pengenalan suara dan sintesis suara hingga peningkatan suara dan musik komputasi.

Bagaimana Cara Kerja Pemrosesan Suara?

Pada intinya, pemrosesan suara melibatkan manipulasi sinyal audio digital. Proses ini biasanya melibatkan langkah-langkah berikut:

1. Akuisisi: Suara di dunia nyata ditangkap menggunakan mikrofon, yang mengubah gelombang suara menjadi sinyal listrik analog.
2. Konversi Analog-ke-Digital: Sinyal analog diubah menjadi representasi digital menggunakan konverter analog-ke-digital (ADC). Langkah ini melibatkan pengambilan sampel sinyal analog pada tingkat tertentu dan kuantisasi setiap sampel ke nilai digital.
3. Pemrosesan Sinyal Digital: Setelah dalam domain digital, berbagai algoritma pemrosesan sinyal digital dapat diterapkan untuk mengekstrak informasi yang relevan, meningkatkan kualitas, atau memanipulasi audio dengan cara tertentu. Algoritma ini dapat berkisar dari yang sederhana, seperti filter yang menghilangkan kebisingan yang tidak diinginkan, hingga yang kompleks, seperti algoritma pembelajaran mesin yang dapat mengenali pola dalam ucapan.
4. Konversi Digital-ke-Analog: Dalam beberapa kasus, sinyal audio yang diproses perlu diubah kembali ke bentuk analog, seperti untuk pemutaran melalui speaker. Ini dicapai menggunakan konverter digital-ke-analog (DAC).

Aplikasi Pemrosesan Suara

Pemrosesan suara memiliki dampak besar pada berbagai industri, menghasilkan berbagai aplikasi yang memengaruhi kehidupan kita sehari-hari. Beberapa aplikasi yang terkenal termasuk:

• Asisten Suara: Asisten yang diaktifkan suara seperti Siri, Alexa, dan Google Assistant sangat bergantung pada pemrosesan suara untuk memahami perintah kita dan menanggapi dengan tepat.
• Pengenalan Ucapan: Teknologi pengenalan ucapan telah merevolusi cara kita berinteraksi dengan perangkat, memungkinkan dikte, pencarian suara, dan kontrol bebas genggam.
• Peningkatan Suara: Algoritma pemrosesan suara digunakan untuk meningkatkan kualitas audio dengan mengurangi kebisingan, menekan gema, dan meningkatkan kejelasan.
• Musik Komputasi: Pemrosesan suara memainkan peran penting dalam pembuatan, pengeditan, dan pemutaran musik digital, yang memungkinkan berbagai efek, instrumen virtual, dan teknik produksi.
• Perawatan Kesehatan: Pemrosesan suara menemukan aplikasi dalam perangkat bantu dengar, diagnosis medis, dan pemantauan pasien, meningkatkan kehidupan individu dengan gangguan pendengaran dan membantu para profesional medis.

Masa Depan Pemrosesan Suara

Karena teknologi terus berkembang, bidang pemrosesan suara siap untuk kemajuan dan aplikasi yang lebih transformatif. Dengan munculnya pembelajaran mesin dan kecerdasan buatan, kita dapat mengharapkan untuk menyaksikan kemampuan yang lebih canggih dan antarmuka yang lebih alami dalam interaksi manusia-komputer. Dari mobil self-driving hingga rumah pintar dan kota pintar, pemrosesan suara tidak diragukan lagi akan memainkan peran penting dalam membentuk masa depan kita.

Representasi Matematis Sinyal Suara

Suara, yang kita dengar dan interpretasikan setiap hari, pada dasarnya merupakan fenomena fisik. Suara tercipta dari getaran suatu objek, yang kemudian merambat melalui medium seperti udara atau air dalam bentuk gelombang. Gelombang ini, yang dikenal sebagai gelombang suara, membawa energi dari sumber suara ke telinga kita.

Untuk memahami suara secara lebih dalam, kita perlu melampaui persepsi indera dan melihat representasi matematisnya. Dalam ranah matematika, sinyal suara direpresentasikan sebagai fungsi waktu. Fungsi ini menggambarkan bagaimana tekanan udara berubah seiring waktu di titik tertentu saat suara merambat melewatinya.

Ada dua cara utama untuk merepresentasikan sinyal suara secara matematis:

1. Domain Waktu: Dalam domain waktu, sinyal suara direpresentasikan sebagai grafik dengan waktu pada sumbu horizontal dan amplitudo (yang merepresentasikan tekanan udara) pada sumbu vertikal. Representasi ini memberikan gambaran jelas tentang bagaimana suara berubah seiring waktu, menunjukkan puncak dan lembah gelombang suara.

2. Domain Frekuensi: Representasi domain frekuensi menguraikan sinyal suara menjadi komponen-komponen frekuensi penyusunnya. Alih-alih menunjukkan perubahan tekanan udara dari waktu ke waktu, representasi ini menunjukkan amplitudo setiap frekuensi yang ada dalam sinyal suara. Hal ini memungkinkan kita untuk memahami “warna” suara, seperti perbedaan antara suara seruling dan gitar, karena instrumen yang berbeda menghasilkan spektrum frekuensi yang berbeda.

Pemahaman tentang representasi matematis sinyal suara ini sangat penting dalam berbagai aplikasi, termasuk:

• Pengolahan Sinyal Digital: Memungkinkan manipulasi suara untuk tujuan seperti kompresi, pengeditan, dan sintesis.
• Pengenalan Suara: Menerjemahkan suara manusia menjadi teks, yang digunakan dalam asisten virtual dan perangkat lunak dikte.
• Analisis Musik: Menganalisis struktur dan konten musik untuk tujuan seperti identifikasi genre dan pembuatan musik otomatis.

Secara keseluruhan, representasi matematis dari sinyal suara memberi kita alat yang ampuh untuk memahami, menganalisis, dan memanipulasi suara. Representasi ini merupakan dasar bagi banyak teknologi modern yang kita andalkan setiap harinya.

Transformasi Fourier: Memecah Belah Suara Menjadi Frekuensi

Pernahkah Anda bertanya-tanya bagaimana aplikasi pengenal suara dapat memahami ucapan Anda, atau bagaimana filter pada aplikasi musik dapat memisahkan vokal dari instrumen? Jawabannya terletak pada konsep matematika yang kuat yang disebut Transformasi Fourier.

Secara sederhana, Transformasi Fourier memungkinkan kita untuk mengambil sinyal, seperti gelombang suara, dan memecahnya menjadi frekuensi penyusunnya. Bayangkan sebuah kue yang terbuat dari berbagai bahan. Transformasi Fourier seperti resep yang memberi tahu kita jumlah yang tepat dari setiap bahan yang digunakan.

Dalam konteks suara, sinyal asli biasanya direpresentasikan sebagai gelombang yang kompleks dalam domain waktu, menunjukkan bagaimana amplitudo suara berubah dari waktu ke waktu. Transformasi Fourier mengubah sinyal ini ke domain frekuensi, menampilkan amplitudo setiap frekuensi yang ada dalam suara.

Representasi domain frekuensi ini sangat berguna dalam berbagai aplikasi. Misalnya:

• Pengenalan Suara: Dengan menganalisis frekuensi yang ada dalam ucapan, algoritma dapat mengidentifikasi kata dan frasa.
• Pemrosesan Musik: Filter dapat digunakan untuk meningkatkan atau menekan frekuensi tertentu, seperti meningkatkan bass atau mengurangi treble.
• Kompresi Data: Dengan membuang frekuensi yang kurang penting, kita dapat mengurangi jumlah data yang diperlukan untuk merepresentasikan sinyal audio.

Meskipun konsep matematika di balik Transformasi Fourier bisa rumit, inti dari ide ini cukup intuitif. Dengan memahami bagaimana suara dipecah menjadi frekuensi penyusunnya, kita dapat membuka banyak kemungkinan dalam berbagai bidang, mulai dari hiburan hingga kedokteran dan lainnya.

Filter Digital: Membersihkan dan Membentuk Suara

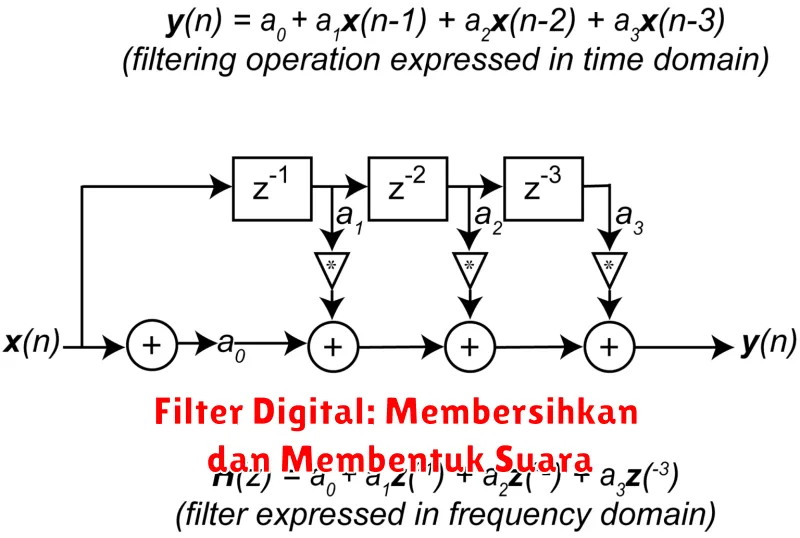
Di dunia audio yang semakin digital, filter digital telah menjadi alat yang esensial untuk memanipulasi dan meningkatkan suara. Dari membersihkan rekaman yang bising hingga membentuk nada instrumen musik, filter digital menawarkan kontrol yang belum pernah ada sebelumnya atas setiap aspek suara.

Pada intinya, filter digital adalah algoritma matematika yang mengubah sinyal audio digital. Mereka bekerja dengan memilih frekuensi tertentu dalam sinyal dan memperkuat atau melemahkannya. Dengan memanipulasi frekuensi ini secara selektif, filter digital dapat mencapai berbagai efek, termasuk:

• Pembersihan Suara: Filter dapat menghilangkan kebisingan yang tidak diinginkan seperti desisan, dengungan, atau suara yang mengganggu dari rekaman, menghasilkan audio yang lebih jernih dan lebih mudah didengarkan.
• Pembentukan Nada: Dengan memperkuat atau memotong frekuensi tertentu, filter dapat mengubah warna nada instrumen musik atau vokal, membuatnya lebih cerah, lebih hangat, atau lebih kuat.
• Efek Khusus: Filter digunakan untuk menciptakan berbagai efek khusus, seperti gema, chorus, dan flanging, yang dapat menambahkan kedalaman, ruang, dan tekstur pada suara.

Ada berbagai jenis filter digital yang tersedia, masing-masing dengan karakteristik dan aplikasi uniknya sendiri. Beberapa jenis yang paling umum termasuk:

1. Filter Low-Pass: Melewati frekuensi rendah dan melemahkan frekuensi tinggi, ideal untuk menghilangkan suara bernada tinggi atau menambahkan kehangatan.
2. Filter High-Pass: Melewati frekuensi tinggi dan melemahkan frekuensi rendah, berguna untuk membersihkan audio yang boomy atau menambahkan kecerahan.
3. Filter Band-Pass: Melewati frekuensi dalam rentang tertentu dan melemahkan frekuensi di luar rentang itu, ideal untuk mengisolasi instrumen atau vokal tertentu dalam campuran.
4. Filter Notch: Melemahkan frekuensi yang sangat spesifik, berguna untuk menghilangkan frekuensi yang tidak diinginkan seperti dengungan saluran listrik.

Filter digital adalah alat yang ampuh yang dapat digunakan untuk meningkatkan dan mengubah suara dalam banyak cara. Memahami berbagai jenis filter dan aplikasinya sangat penting bagi siapa saja yang ingin memaksimalkan potensi audio mereka, baik itu produser musik, insinyur audio, atau hanya penggemar musik biasa.

Peran Algoritma dalam Kompresi Audio

Di era digital ini, kita dikelilingi oleh data dalam berbagai bentuk, salah satunya adalah audio. Dari musik dan podcast hingga panggilan konferensi dan video game, audio telah menjadi bagian integral dari kehidupan kita. Namun, file audio mentah bisa sangat besar, membutuhkan banyak ruang penyimpanan dan bandwidth untuk ditransmisikan atau dialirkan.

Di sinilah peran penting kompresi audio. Kompresi audio adalah proses mengurangi ukuran file audio tanpa mengorbankan kualitas suara secara signifikan. Hal ini dicapai dengan menggunakan algoritma cerdas yang mengidentifikasi dan menghilangkan data yang berlebihan atau tidak perlu dalam sinyal audio.

Algoritma adalah jantung dari kompresi audio. Mereka adalah serangkaian instruksi matematika yang memandu proses kompresi dan dekompresi. Ada banyak jenis algoritma kompresi audio, masing-masing dengan kekuatan dan kelemahannya sendiri. Beberapa algoritma dirancang untuk kompresi lossless, yang berarti tidak ada kehilangan kualitas audio sama sekali. Algoritma ini ideal untuk situasi di mana mempertahankan keaslian audio sangat penting, seperti pengarsipan musik atau produksi audio profesional.

Di sisi lain, algoritma lossy memang menghilangkan beberapa data audio selama kompresi. Namun, algoritma ini dirancang untuk melakukannya dengan cara yang tidak terlalu terlihat oleh telinga manusia. Algoritma lossy memungkinkan tingkat kompresi yang jauh lebih tinggi daripada algoritma lossless, menjadikannya ideal untuk streaming musik, podcast, dan penggunaan lainnya di mana ukuran file kecil lebih diutamakan.

Beberapa contoh algoritma kompresi audio yang populer termasuk:

• MP3 (MPEG-1 Audio Layer 3): Algoritma lossy yang banyak digunakan yang menawarkan kompresi tinggi dengan sedikit penurunan kualitas yang nyata.
• AAC (Advanced Audio Coding): Algoritma lossy lain yang dikenal dengan kualitasnya yang lebih baik daripada MP3 pada bitrate yang sama.
• FLAC (Free Lossless Audio Codec): Algoritma lossless yang populer yang menyediakan kompresi tanpa kehilangan kualitas audio.
• ALAC (Apple Lossless Audio Codec): Algoritma lossless yang dikembangkan oleh Apple yang menawarkan kompresi serupa dengan FLAC.

Pemilihan algoritma kompresi audio tergantung pada kebutuhan dan preferensi spesifik. Faktor-faktor yang perlu dipertimbangkan termasuk tingkat kompresi yang diinginkan, kualitas audio yang dapat diterima, dan sumber daya komputasi yang tersedia.

Kesimpulannya, algoritma memainkan peran penting dalam kompresi audio, memungkinkan kita untuk menikmati audio berkualitas tinggi sambil meminimalkan kebutuhan ruang penyimpanan dan bandwidth. Seiring dengan kemajuan teknologi, kita dapat mengharapkan algoritma kompresi audio yang lebih canggih dan efisien yang semakin memperkecil batas antara audio digital dan aslinya.

Penerapan Matematika dalam Pengenalan Suara Otomatis

Pengenalan suara otomatis, atau Automatic Speech Recognition (ASR), telah menjadi teknologi yang semakin penting dalam kehidupan sehari-hari. Dari asisten virtual seperti Siri dan Google Assistant hingga sistem dikte dan perangkat rumah pintar, ASR memungkinkan kita untuk berinteraksi dengan teknologi menggunakan suara kita. Di balik teknologi canggih ini, terdapat peran penting dari matematika, khususnya dalam pemrosesan sinyal, statistik, dan pembelajaran mesin.

Pemrosesan Sinyal: Suara pada dasarnya adalah gelombang yang merambat di udara. Tahap pertama dalam ASR adalah mengubah gelombang suara ini menjadi representasi digital yang dapat diproses oleh komputer. Di sinilah pemrosesan sinyal digital berperan. Teknik seperti Fast Fourier Transform (FFT) digunakan untuk menguraikan sinyal suara kompleks menjadi komponen frekuensi individual, yang memungkinkan sistem untuk mengidentifikasi pola dan fitur penting dalam suara.

Statistik: Setelah sinyal suara diubah menjadi representasi digital, langkah selanjutnya adalah mengekstrak fitur-fitur yang relevan untuk pengenalan suara. Fitur-fitur ini, seperti Mel-Frequency Cepstral Coefficients (MFCCs), menangkap karakteristik akustik unik dari suara yang berbeda. Statistik memainkan peran penting dalam menganalisis fitur-fitur ini dan membangun model statistik yang mewakili fonem atau unit suara dasar dalam suatu bahasa. Model statistik ini, seperti Hidden Markov Models (HMMs), memungkinkan sistem untuk memprediksi urutan fonem yang paling mungkin berdasarkan fitur-fitur yang diekstraksi dari sinyal suara.

Pembelajaran Mesin: Dalam beberapa tahun terakhir, pembelajaran mesin, khususnya deep learning, telah merevolusi bidang pengenalan suara otomatis. Jaringan saraf tiruan, seperti Recurrent Neural Networks (RNNs) dan Transformers, mampu mempelajari pola kompleks dalam data suara dengan akurasi yang belum pernah terjadi sebelumnya. Model-model ini dilatih pada dataset besar yang berisi rekaman suara dan transkripsi teksnya, memungkinkan mereka untuk menggeneralisasi dengan baik ke data yang tidak terlihat sebelumnya. Algoritma pembelajaran mesin terus disempurnakan dan memainkan peran yang semakin penting dalam meningkatkan akurasi dan ketahanan sistem ASR di berbagai lingkungan dan aksen.

Singkatnya, penerapan matematika dalam pengenalan suara otomatis sangatlah penting. Dari pemrosesan sinyal hingga statistik dan pembelajaran mesin, konsep matematika membentuk dasar dari teknologi canggih ini. Seiring dengan kemajuan dalam bidang-bidang ini, kita dapat berharap untuk melihat sistem ASR yang lebih akurat, andal, dan mudah diakses di masa depan.