Machine learning telah menjadi pusat perhatian di dunia teknologi, merevolusi berbagai industri dengan kemampuannya untuk belajar dari data dan membuat prediksi. Dari mobil self-driving hingga rekomendasi produk yang dipersonalisasi, algoritma machine learning semakin canggih. Tapi tahukah Anda kekuatan pendorong di balik kecerdasan buatan yang transformatif ini? Jawabannya terletak pada cabang matematika yang mungkin pernah Anda takuti di bangku kuliah: kalkulus.
Artikel ini akan mengungkap peran penting kalkulus dalam membentuk lanskap machine learning. Kita akan menjelajahi bagaimana konsep-konsep kalkulus seperti turunan dan integral menjadi pondasi bagi algoritma pembelajaran mesin untuk mempelajari pola, mengoptimalkan model, dan pada akhirnya, membuat prediksi yang akurat. Bersiaplah untuk menyelami dunia matematika yang menarik dan memahami bagaimana kalkulus memberdayakan revolusi machine learning.
Dasar-Dasar Kalkulus untuk Machine Learning

Machine learning, cabang yang menarik dari kecerdasan buatan, telah merevolusi berbagai industri. Dari mobil self-driving hingga rekomendasi yang dipersonalisasi, algoritma machine learning mampu mengekstrak pola dari data dan membuat prediksi. Di balik algoritma yang kuat ini terletak dasar matematika yang kuat, dan kalkulus memainkan peran penting.
Artikel ini membahas konsep dasar kalkulus yang penting untuk memahami algoritma machine learning. Apakah Anda seorang pemula atau yang ingin menyegarkan pengetahuan Anda, artikel ini akan memberi Anda pemahaman yang jelas tentang prinsip-prinsip kalkulus utama yang digunakan dalam machine learning.
1. Derivatif
Derivatif mengukur laju perubahan suatu fungsi terhadap variabel inputnya. Dalam machine learning, derivatif digunakan untuk menemukan nilai optimal dari parameter model selama pelatihan. Algoritma Gradient Descent, metode pengoptimalan yang banyak digunakan, menggunakan derivatif untuk secara iteratif memperbarui parameter model dan meminimalkan fungsi biaya.
2. Gradien
Gradien adalah vektor yang menunjukkan arah laju perubahan terbesar dari suatu fungsi. Dalam konteks fungsi multivariabel, gradien menunjuk ke arah pendakian tercuram. Dalam machine learning, gradien digunakan untuk menemukan arah penurunan tercuram dari fungsi biaya, membimbing algoritma pengoptimalan menuju nilai parameter optimal.
3. Aturan Rantai
Aturan rantai adalah aturan penting dalam kalkulus yang memungkinkan kita menghitung turunan dari fungsi komposit. Dalam jaringan saraf, di mana beberapa fungsi disusun bersama, aturan rantai digunakan untuk menghitung gradien yang dipropagasikan kembali melalui jaringan selama Backpropagation, memungkinkan penyesuaian bobot.
4. Integral
Integral adalah kebalikan dari derivatif. Integral menghitung luas di bawah kurva suatu fungsi. Dalam machine learning, integral digunakan dalam berbagai aplikasi, seperti menghitung probabilitas dari fungsi kepadatan probabilitas dan menentukan nilai yang diharapkan dari variabel acak.
5. Fungsi Multivariabel dan Turunan Parsial
Machine learning seringkali berhubungan dengan dataset multidimensi. Fungsi multivariabel adalah fungsi yang memiliki banyak input. Turunan parsial memungkinkan kita untuk menghitung laju perubahan suatu fungsi multivariabel terhadap satu variabel input, dengan mempertahankan variabel lainnya sebagai konstanta.
Kesimpulan
Kalkulus adalah dasar matematika untuk memahami dan mengembangkan algoritma machine learning. Konsep-konsep seperti derivatif, gradien, aturan rantai, integral, dan fungsi multivariabel sangat penting untuk pengoptimalan model, propagasi balik, dan tugas-tugas penting lainnya dalam machine learning. Dengan memahami prinsip-prinsip kalkulus ini, Anda dapat memperdalam pengetahuan Anda tentang machine learning dan membuka kekuatan algoritma yang kompleks.
Turunan: Mencari Kemiringan Fungsi Kerugian

Dalam dunia pembelajaran mesin, kita sering dihadapkan dengan tugas untuk menemukan serangkaian parameter yang meminimalkan fungsi kerugian. Fungsi kerugian mengukur seberapa baik model kita dalam memprediksi data yang diberikan. Salah satu alat paling penting yang kita gunakan untuk mencapai hal ini adalah turunan.
Bayangkan fungsi kerugian sebagai permukaan berbukit. Tujuan kita adalah menemukan titik terendah di permukaan ini, yang mewakili himpunan parameter yang memberikan kesalahan terkecil. Turunan memberi tahu kita kemiringan permukaan pada titik tertentu. Dengan mengikuti arah penurunan tercuram (gradien negatif), kita dapat secara bertahap mencapai titik minimum.
Cara kerjanya:
- Kita mulai dengan tebakan awal untuk parameter model kita.
- Kita menghitung turunan fungsi kerugian terhadap setiap parameter.
- Turunan ini memberi tahu kita arah dan besarnya perubahan yang perlu kita lakukan pada setiap parameter untuk mengurangi nilai fungsi kerugian.
- Kita memperbarui parameter kita dengan menggerakkannya sedikit ke arah penurunan tercuram, yang ditentukan oleh turunannya.
- Kita mengulangi langkah 2-4 hingga fungsi kerugian mencapai nilai minimum atau berhenti menurun secara signifikan.
Proses ini dikenal sebagai gradient descent dan membentuk dasar dari banyak algoritma pembelajaran mesin. Pemahaman yang kuat tentang turunan sangat penting untuk memahami dan menerapkan algoritma ini secara efektif.
Singkatnya, turunan memainkan peran penting dalam pembelajaran mesin dengan memungkinkan kita untuk menemukan himpunan parameter yang meminimalkan fungsi kerugian. Dengan memberi tahu kita kemiringan fungsi kerugian pada titik tertentu, turunan memandu kita menuju minimum, sehingga meningkatkan akurasi dan efektivitas model kita.
Gradien: Menuju Titik Minimum Fungsi

Dalam dunia optimisasi, terutama dalam konteks machine learning, menemukan titik minimum suatu fungsi merupakan tujuan utama. Titik minimum merepresentasikan solusi optimal, seperti parameter model terbaik atau konfigurasi sistem yang paling efisien. Di sinilah peran gradien menjadi krusial.
Bayangkan diri Anda berdiri di lereng gunung. Tujuan Anda adalah mencapai dasar lembah. Cara intuitif adalah dengan selalu melangkah ke arah yang paling curam ke bawah. Inilah esensi dari gradien! Secara matematis, gradien menunjukkan arah dan besarnya perubahan tercuram dari suatu fungsi pada titik tertentu.
Algoritma optimisasi, seperti Gradient Descent, memanfaatkan informasi gradien ini. Dimulai dari titik awal, algoritma secara iteratif menggeser titik tersebut ke arah negatif gradien. Analogi gunung kembali relevan: Anda terus melangkah ke arah turunan tercuram hingga mencapai dasar lembah. Proses ini berulang hingga mencapai titik di mana gradien mendekati nol, mengindikasikan titik minimum (atau setidaknya titik stasioner).
Penting untuk diingat bahwa gradien hanyalah alat. Kompleksitas fungsi (bisa jadi memiliki banyak lembah!) dan pemilihan parameter algoritma (seperti learning rate atau momentum) mempengaruhi efektivitasnya. Terkadang, Anda mungkin terjebak di lembah lokal, bukan mencapai lembah terdalam (minimum global).
Meskipun demikian, pemahaman tentang gradien dan bagaimana algoritma memanfaatkannya merupakan fondasi penting dalam memahami optimisasi dan machine learning.
Optimasi Model dengan Algoritma Gradient Descent
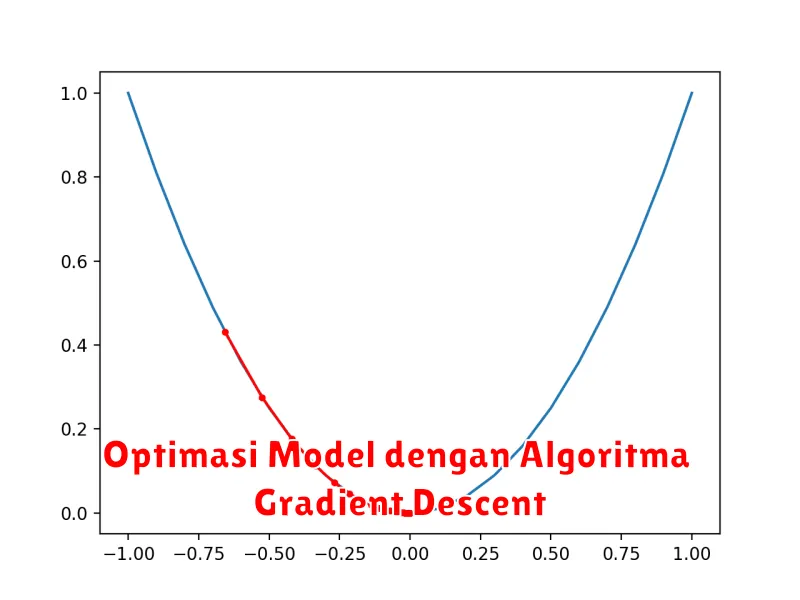
Dalam dunia machine learning, membangun model prediktif yang akurat merupakan tujuan utama. Proses ini melibatkan pencarian serangkaian parameter model yang mengoptimalkan kemampuan model dalam mempelajari pola dari data. Di sinilah peran penting algoritma optimasi, dan salah satu yang paling populer adalah Gradient Descent.
Secara sederhana, bayangkan Anda berada di puncak gunung dan ingin turun ke lembah secepat mungkin. Gradient Descent seperti pemandu yang membantu Anda menuruni gunung dengan langkah-langkah kecil menuju arah penurunan tercuram. Dalam konteks machine learning, “gunung” tersebut merepresentasikan fungsi kerugian (loss function) yang mengukur kesalahan prediksi model, dan “lembah” adalah titik minimum fungsi kerugian, yang mengindikasikan model dengan performa terbaik.
Algoritma ini bekerja dengan menghitung gradien dari fungsi kerugian terhadap setiap parameter model. Gradien menunjukkan arah dan besarnya perubahan fungsi kerugian terhadap perubahan parameter. Dengan informasi ini, Gradient Descent secara iteratif memperbarui parameter model dengan bergerak ke arah yang berlawanan dengan gradien, mengurangi kesalahan prediksi sedikit demi sedikit hingga mencapai titik minimum atau mendekati.
Terdapat beberapa varian Gradient Descent, seperti Batch Gradient Descent yang menggunakan seluruh data untuk setiap pembaruan parameter, Stochastic Gradient Descent yang menggunakan satu sampel data acak, dan Mini-Batch Gradient Descent yang menggabungkan keduanya dengan menggunakan sebagian kecil data acak. Setiap varian memiliki kelebihan dan kelemahan, dan pemilihannya bergantung pada karakteristik data dan kompleksitas model.
Meskipun tergolong sederhana, Gradient Descent telah menjadi fondasi bagi banyak algoritma optimasi yang lebih kompleks dan powerful. Kemampuannya dalam menemukan solusi optimal untuk berbagai model machine learning menjadikannya salah satu algoritma yang wajib dipahami dalam membangun model prediktif yang handal.
Aplikasi Kalkulus dalam Jaringan Saraf Tiruan

Jaringan saraf tiruan (JST) telah menjadi salah satu teknologi paling transformatif dalam beberapa tahun terakhir, yang mendorong kemajuan di berbagai bidang seperti pengenalan gambar, pemrosesan bahasa alami, dan kendaraan otonom. Di balik kerumitan JST terdapat konsep matematika yang mendalam, dan kalkulus memainkan peran penting dalam memahami dan mengembangkan algoritma pembelajaran yang memberdayakan sistem cerdas ini.
Pada intinya, JST bertujuan untuk meniru kemampuan otak manusia dalam mempelajari pola dan membuat prediksi dari data. Mereka terdiri dari node yang saling berhubungan yang diatur dalam lapisan, yang masing-masing melakukan operasi matematika sederhana. Proses pembelajaran melibatkan penyesuaian bobot, atau parameter, dari koneksi ini untuk meminimalkan perbedaan antara prediksi jaringan dan nilai yang sebenarnya.
Di sinilah kalkulus berperan. Turunan, konsep fundamental dalam kalkulus, memungkinkan kita untuk mengukur bagaimana perubahan input suatu fungsi mempengaruhi outputnya. Dalam konteks JST, turunan digunakan untuk menghitung gradien dari fungsi biaya, yang mengukur kinerja jaringan. Gradien menunjukkan arah dan besarnya perubahan bobot yang akan meminimalkan kesalahan jaringan.
Algoritma yang paling umum digunakan untuk melatih JST disebut algoritma penurunan gradien. Algoritma ini menggunakan turunan untuk secara iteratif memperbarui bobot jaringan, bergerak menuruni gradien fungsi biaya. Dengan mengulangi proses ini, jaringan secara bertahap meningkatkan akurasinya dalam membuat prediksi.
Selain penurunan gradien, kalkulus juga mendasari teknik optimasi lanjutan yang digunakan untuk meningkatkan proses pelatihan JST. Misalnya, algoritma optimasi berbasis momentum menggunakan konsep turunan orde pertama dan kedua untuk mempercepat konvergensi dan menghindari minima lokal. Demikian pula, metode regularisasi, yang mencegah overfitting dengan menambahkan batasan pada bobot jaringan, juga bergantung pada konsep kalkulus.
Singkatnya, kalkulus merupakan dasar matematika untuk memahami dan mengembangkan algoritma pembelajaran yang memberdayakan JST. Turunan, khususnya, memainkan peran penting dalam menghitung gradien, yang memandu proses optimasi bobot jaringan. Seiring dengan kemajuan JST, pemahaman yang kuat tentang kalkulus akan menjadi semakin penting bagi siapa pun yang ingin merancang, menerapkan, atau meneliti sistem cerdas ini.