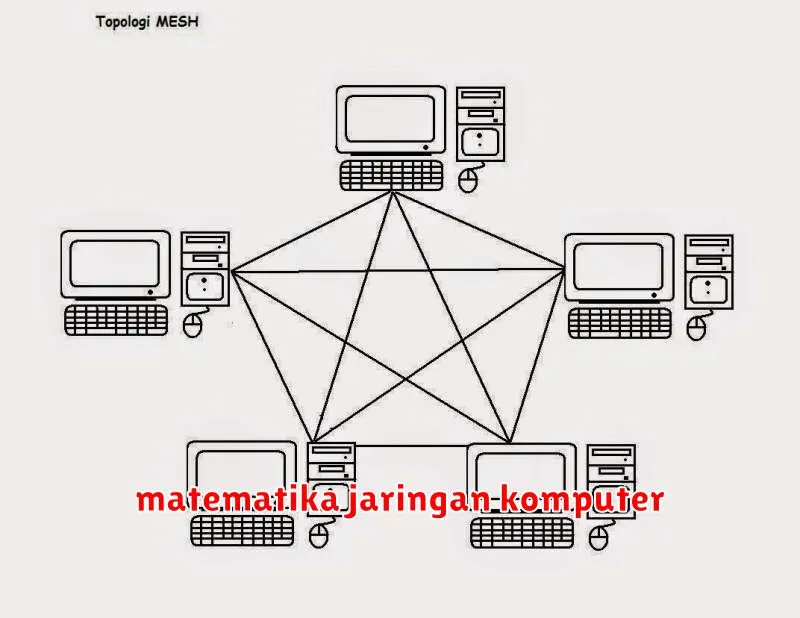
Di era digital yang semakin maju ini, jaringan komputer telah menjadi tulang punggung kehidupan modern. Dari aktivitas sehari-hari seperti browsing internet dan media sosial hingga operasi bisnis yang kompleks, semuanya bergantung pada kelancaran dan efisiensi jaringan. Namun, tahukah Anda bahwa di balik layar, matematika memainkan peran penting dalam analisis jaringan komputer yang memastikan kinerja optimal?
Artikel ini akan menguak rahasia bagaimana matematika berperan sebagai ‘otak’ di balik kelancaran jaringan komputer. Kita akan menjelajahi konsep-konsep matematika seperti teori graf, probabilitas, dan statistik yang menjadi dasar dalam menganalisis performa jaringan, mengidentifikasi hambatan, dan mengoptimalkan efisiensi. Mari kita telaah lebih dalam bagaimana ‘bahasa angka’ ini menjadi kunci dalam memahami dan menguasai dunia jaringan komputer yang kompleks.
Pendahuluan: Jaringan Komputer dan Kompleksitasnya
Di era digital ini, jaringan komputer telah menjadi tulang punggung masyarakat modern. Dari interaksi sosial media hingga transaksi perbankan online, hampir setiap aspek kehidupan kita terhubung melalui jaringan yang rumit ini. Namun, di balik kenyamanan yang ditawarkan, tersembunyi kompleksitas yang menakjubkan.
Bayangkan sebuah jaringan komputer sebagai sebuah kota yang hidup. Perangkat seperti komputer, smartphone, dan server adalah bangunannya, sementara protokol komunikasi adalah aturan lalu lintas yang mengatur arus informasi. Seperti halnya kota yang terus berkembang, jaringan komputer juga terus bertumbuh, menambahkan perangkat dan koneksi baru, yang semakin menambah kompleksitasnya.
Memahami kompleksitas ini penting, tidak hanya bagi para profesional di bidang teknologi, tetapi juga bagi masyarakat luas. Dengan pemahaman yang lebih baik, kita dapat memanfaatkan kekuatan jaringan komputer secara lebih efektif, sambil memitigasi risiko dan tantangan yang mungkin muncul.
Di era digital yang semakin maju ini, data mengalir seperti sungai yang deras. Setiap klik, setiap pencarian, setiap transaksi daring menghasilkan data yang tak terhitung jumlahnya. Fenomena ini memunculkan istilah “arus data”, yang merujuk pada aliran data yang terus-menerus dan berkelanjutan.
Memahami arus data menjadi sangat penting bagi berbagai bidang, mulai dari bisnis dan teknologi hingga ilmu pengetahuan dan pemerintahan. Di sinilah peran matematika muncul sebagai kunci utama. Matematika menyediakan kerangka kerja dan alat yang diperlukan untuk mengolah, menganalisis, dan memahami kompleksitas arus data.
Peran Statistik dalam Menganalisis Arus Data
Statistik, cabang matematika yang berfokus pada pengumpulan, pengorganisasian, analisis, interpretasi, dan penyajian data, memiliki peran sentral dalam mengelola arus data. Dengan menggunakan metode statistik, kita dapat:
- Mengidentifikasi pola dan tren: Statistik membantu kita menemukan pola tersembunyi dan tren signifikan dalam data yang tampaknya acak. Ini memungkinkan kita untuk membuat prediksi dan mengambil keputusan yang lebih tepat.
- Menguji hipotesis: Statistik memungkinkan kita untuk menguji validitas asumsi dan hipotesis tentang data. Hal ini membantu kita untuk memvalidasi atau menolak teori dan membangun pemahaman yang lebih baik tentang fenomena yang sedang dipelajari.
- Membuat model prediktif: Dengan menggunakan teknik statistik seperti regresi dan machine learning, kita dapat membangun model yang dapat memprediksi hasil di masa depan berdasarkan data historis.
Aljabar Linear dan Pengolahan Data Masif
Aljabar linear, yang berfokus pada vektor, matriks, dan sistem persamaan linear, memainkan peran penting dalam pengolahan data masif. Arus data sering direpresentasikan dalam bentuk matriks berdimensi tinggi, dan aljabar linear menyediakan alat yang efisien untuk:
- Reduksi dimensi: Mengurangi kompleksitas data dengan mengidentifikasi dan mempertahankan informasi yang paling relevan.
- Dekomposisi matriks: Mengurai matriks data menjadi komponen-komponen yang lebih sederhana untuk analisis yang lebih mudah.
- Pemecahan sistem persamaan linear: Memecahkan sistem persamaan linear yang besar dan kompleks yang muncul dalam berbagai aplikasi arus data.
Kalkulus dan Analisis Data Real-Time
Dalam konteks arus data real-time, kalkulus menjadi alat yang tak ternilai. Kalkulus memungkinkan kita untuk menganalisis data yang terus berubah seiring waktu. Turunan dan integral, konsep dasar dalam kalkulus, dapat digunakan untuk:
- Mengukur laju perubahan: Menentukan seberapa cepat data berubah dari waktu ke waktu.
- Menghitung nilai akumulasi: Menentukan total nilai data selama periode waktu tertentu.
- Mendeteksi anomali: Mengidentifikasi titik data yang menyimpang secara signifikan dari pola yang diharapkan, yang mungkin mengindikasikan peristiwa atau anomali yang tidak biasa.
Secara keseluruhan, matematika adalah fondasi yang kuat untuk memahami dan memanfaatkan potensi penuh arus data. Dengan menguasai konsep dan teknik matematika yang relevan, kita dapat membuka wawasan yang berharga, membuat keputusan yang lebih baik, dan mendorong inovasi di berbagai bidang.
Teori Graf: Memvisualisasikan Jaringan yang Rumit
Dalam dunia yang semakin terhubung ini, memahami jaringan yang kompleks menjadi sangat penting. Dari jejaring sosial hingga sistem transportasi, jaringan ada di sekitar kita, menghubungkan orang, tempat, dan informasi. Teori graf muncul sebagai alat yang ampuh untuk memodelkan dan menganalisis jaringan ini, memungkinkan kita untuk mengungkap pola tersembunyi, mengidentifikasi hubungan penting, dan membuat keputusan yang tepat.
Pada intinya, graf adalah representasi visual dari suatu jaringan. Ini terdiri dari simpul (juga dikenal sebagai titik atau node), yang mewakili entitas dalam jaringan, dan sisi (juga dikenal sebagai garis atau arc), yang mewakili hubungan antara entitas tersebut. Misalnya, dalam jejaring sosial, pengguna dapat direpresentasikan sebagai simpul, dan pertemanan mereka dapat direpresentasikan sebagai sisi.
Keindahan teori graf terletak pada kesederhanaannya dan fleksibilitasnya. Dengan hanya menggunakan simpul dan sisi, kita dapat memodelkan berbagai macam jaringan, terlepas dari kompleksitasnya. Selain itu, teori graf menyediakan seperangkat algoritma dan metrik yang kaya untuk menganalisis jaringan ini, yang memungkinkan kita untuk menjawab pertanyaan seperti:
- Apa jalur terpendek antara dua simpul dalam jaringan?
- Simpul mana yang paling berpengaruh dalam jaringan?
- Bagaimana informasi menyebar melalui jaringan?
Aplikasi teori graf sangat luas, mencakup berbagai bidang seperti:
- Ilmu komputer: Jaringan komputer, algoritma grafik, basis data grafik
- Ilmu sosial: Analisis jejaring sosial, dinamika kelompok, penyebaran informasi
- Transportasi: Perencanaan rute, optimasi lalu lintas, logistik
- Biologi: Interaksi protein-protein, jaringan metabolik, ilmu saraf
- Keuangan: Analisis risiko, deteksi penipuan, optimasi portofolio
Sebagai kesimpulan, teori graf adalah alat yang sangat berharga untuk memahami dan menganalisis jaringan yang kompleks. Dengan merepresentasikan jaringan sebagai graf, kita dapat menggunakan alat matematika dan algoritma untuk mengungkap wawasan tersembunyi, membuat prediksi, dan mengoptimalkan sistem. Saat kita memasuki era data besar dan konektivitas yang terus meningkat, teori graf pasti akan memainkan peran yang semakin penting dalam membantu kita menavigasi kompleksitas dunia kita.
Aljabar Linear: Memecahkan Persamaan Jaringan
Aljabar linear adalah cabang matematika yang sangat penting dengan aplikasi yang luas di berbagai bidang, termasuk ilmu komputer, fisika, dan teknik. Salah satu aplikasi yang menarik adalah kemampuannya untuk memecahkan persamaan jaringan. Dalam artikel ini, kita akan menjelajahi bagaimana konsep aljabar linear dapat digunakan untuk menganalisis dan memecahkan sistem persamaan linear yang merepresentasikan jaringan.
Memahami Jaringan dan Persamaan
Jaringan, dalam konteks ini, mengacu pada kumpulan node atau titik yang saling terhubung oleh cabang atau edge. Jaringan dapat merepresentasikan berbagai sistem dunia nyata, seperti sirkuit listrik, jaringan transportasi, atau bahkan jaringan sosial. Perilaku jaringan ini seringkali dapat dimodelkan menggunakan sistem persamaan linear, di mana setiap persamaan mewakili hubungan antara variabel yang terkait dengan node atau cabang.
Peran Matriks dan Vektor
Aljabar linear menyediakan alat yang ampuh untuk merepresentasikan dan memanipulasi sistem persamaan linear menggunakan matriks dan vektor. Matriks adalah larik angka yang disusun dalam baris dan kolom, sedangkan vektor adalah matriks dengan satu kolom. Dalam konteks persamaan jaringan:
- Matriks dapat digunakan untuk merepresentasikan koefisien variabel dalam persamaan.
- Vektor dapat digunakan untuk merepresentasikan variabel itu sendiri atau nilai konstan.
Metode Penyelesaian
Setelah sistem persamaan jaringan direpresentasikan dalam bentuk matriks, berbagai metode aljabar linear dapat digunakan untuk menyelesaikan nilai variabel yang tidak diketahui. Beberapa metode umum meliputi:
- Eliminasi Gauss: Metode ini melibatkan operasi baris pada matriks augmented (matriks yang mencakup koefisien dan konstanta) untuk mengubahnya menjadi bentuk eselon baris, yang memfasilitasi penyelesaian.
- Dekomposisi Matriks: Teknik seperti dekomposisi LU atau dekomposisi Cholesky menguraikan matriks menjadi bentuk yang lebih sederhana, sehingga lebih mudah untuk menyelesaikan sistem persamaan.
- Metode Iteratif: Metode seperti metode Jacobi atau metode Gauss-Seidel menyelesaikan solusi perkiraan dengan secara iteratif menyempurnakan tebakan awal hingga konvergensi tercapai.
Kesimpulan
Aljabar linear menyediakan kerangka kerja yang kuat dan elegan untuk memecahkan persamaan jaringan. Dengan merepresentasikan sistem ini menggunakan matriks dan vektor, kita dapat memanfaatkan metode aljabar linear untuk mendapatkan solusi yang efisien dan akurat. Pemahaman tentang konsep-konsep ini sangat penting bagi para profesional di berbagai bidang yang berhubungan dengan analisis dan desain jaringan.
Probabilitas dan Statistik: Memprediksi Perilaku Jaringan
Dalam dunia yang semakin terhubung, memahami perilaku jaringan menjadi sangat penting. Baik itu jaringan telekomunikasi, jaringan sosial, atau jaringan transportasi, memprediksi bagaimana jaringan akan berperilaku di bawah kondisi yang berbeda merupakan hal yang krusial untuk pengoptimalan dan pengambilan keputusan.
Di sinilah peran probabilitas dan statistik bermain. Dengan menggunakan prinsip-prinsip matematika ini, kita dapat menganalisis pola, mengukur ketidakpastian, dan membuat prediksi tentang bagaimana informasi dan entitas bergerak dalam jaringan.
Probabilitas dalam Jaringan
Probabilitas memungkinkan kita untuk mengukur kemungkinan suatu peristiwa terjadi dalam konteks jaringan. Contohnya:
- Probabilitas sebuah pesan berhasil dikirim melalui jaringan yang rawan error.
- Probabilitas seorang pengguna mengklik tautan tertentu di situs web.
- Probabilitas suatu node dalam jaringan mengalami kegagalan.
Dengan memahami probabilitas peristiwa-peristiwa ini, kita dapat merancang strategi untuk meningkatkan keandalan, mengoptimalkan kinerja, dan memitigasi risiko.
Statistik dalam Analisis Jaringan
Statistik memberi kita alat untuk meringkas dan menganalisis data jaringan, memungkinkan kita untuk mengidentifikasi pola dan tren yang mendasari.
Misalnya, dengan menggunakan statistik, kita dapat:
- Menganalisis pola lalu lintas jaringan untuk mengidentifikasi jam sibuk dan merencanakan kapasitas.
- Mendeteksi anomali dalam data jaringan yang mungkin mengindikasikan serangan atau kegagalan.
- Membuat model prediktif untuk memperkirakan pertumbuhan jaringan dan kebutuhan sumber daya di masa mendatang.
Kesimpulan
Probabilitas dan statistik adalah alat yang ampuh untuk memahami dan memprediksi perilaku jaringan. Dengan memanfaatkan teknik-teknik ini, kita dapat membuat keputusan yang lebih tepat, meningkatkan kinerja jaringan, dan membuka peluang baru dalam berbagai bidang.
Seiring dengan semakin kompleksnya jaringan di dunia kita, pentingnya probabilitas dan statistik dalam analisis jaringan hanya akan semakin meningkat di masa depan.
Penerapan Konkret: Optimasi Performa Jaringan
Dalam era digital yang serba cepat ini, performa jaringan yang optimal menjadi suatu keharusan. Koneksi yang lambat dan tidak stabil dapat menghambat produktivitas, mengganggu komunikasi, dan menyebabkan frustrasi. Untungnya, ada berbagai langkah konkret yang dapat diambil untuk meningkatkan performa jaringan Anda.
Salah satu langkah pertama yang penting adalah mengidentifikasi akar permasalahan. Apakah koneksi lambat terjadi secara terus-menerus atau hanya pada waktu-waktu tertentu? Apakah masalahnya terletak pada perangkat keras, perangkat lunak, atau penyedia layanan internet Anda? Dengan memahami sumber masalahnya, Anda dapat fokus pada solusi yang tepat.
Selanjutnya, pertimbangkan untuk meningkatkan infrastruktur jaringan Anda. Router dan switch yang usang dapat menjadi hambatan bagi kecepatan dan keandalan jaringan. Pertimbangkan untuk meng-upgrade ke perangkat keras yang lebih baru yang mendukung teknologi terbaru, seperti Wi-Fi 6.
Manajemen bandwidth juga merupakan faktor penting. Jika Anda memiliki banyak perangkat yang terhubung ke jaringan secara bersamaan, memprioritaskan lalu lintas data dapat membuat perbedaan besar. Misalnya, Anda dapat memprioritaskan lalu lintas dari aplikasi konferensi video untuk memastikan kualitas panggilan yang lancar.
Jangan lupakan pentingnya keamanan jaringan. Serangan malware dan ancaman keamanan lainnya dapat secara signifikan memengaruhi performa jaringan. Pastikan Anda memiliki firewall yang kuat dan perangkat lunak antivirus yang selalu diperbarui untuk melindungi jaringan dari penyusup.
Terakhir, pemantauan jaringan secara teratur sangat penting untuk menjaga performa yang optimal. Gunakan alat pemantauan jaringan untuk melacak metrik penting, seperti penggunaan bandwidth, latensi, dan kehilangan paket. Dengan memantau jaringan Anda secara proaktif, Anda dapat mengidentifikasi dan mengatasi potensi masalah sebelum menjadi masalah besar.
Dengan menerapkan langkah-langkah konkret ini, Anda dapat secara signifikan meningkatkan performa jaringan Anda, memastikan konektivitas yang cepat, andal, dan aman untuk semua kebutuhan digital Anda.
Tantangan Masa Depan: Big Data dan Kompleksitas yang Meningkat
Di era digital yang terus berkembang ini, kita dihadapkan pada ledakan data yang belum pernah terjadi sebelumnya. Setiap klik, setiap transaksi, setiap interaksi online menghasilkan jejak data yang semakin memperkaya lautan informasi yang kita kenal sebagai Big Data. Fenomena ini, meski menjanjikan peluang luar biasa, juga menghadirkan tantangan yang semakin kompleks.
Salah satu tantangan utama adalah volume data itu sendiri. Jumlah data yang dihasilkan setiap harinya begitu besar sehingga sulit untuk dibayangkan, apalagi diolah dengan metode tradisional. Tantangan selanjutnya terletak pada kecepatan data. Informasi mengalir tanpa henti, menuntut kemampuan pemrosesan dan analisis yang real-time agar tetap relevan.
Selain volume dan kecepatan, variasi data juga menjadi tantangan tersendiri. Big Data tidak hanya hadir dalam bentuk teks dan angka, tetapi juga gambar, video, audio, dan data sensorik lainnya. Kemampuan untuk mengintegrasikan dan menganalisis berbagai jenis data ini menjadi kunci untuk mengungkap wawasan yang bermakna.
Kompleksitas Big Data semakin meningkat dengan adanya isu veracity, yaitu tingkat keakuratan dan keandalan data. Dalam lautan informasi yang luas ini, tidak semua data diciptakan sama. Memastikan keakuratan dan keandalan data menjadi krusial sebelum mengambil keputusan penting.
Mengatasi tantangan Big Data membutuhkan pendekatan yang komprehensif. Kita perlu mengembangkan infrastruktur teknologi yang mampu menangani volume, kecepatan, dan variasi data yang terus meningkat. Selain itu, dibutuhkan pula talenta-talenta yang terampil dalam bidang analisis data, mampu mengolah informasi menjadi insight yang actionable.
Tantangan Big Data bukanlah halangan, melainkan peluang untuk berinovasi dan berkembang. Dengan strategi yang tepat dan kolaborasi lintas disiplin, kita dapat memanfaatkan kekuatan Big Data untuk menciptakan solusi inovatif bagi berbagai sektor, membuka jalan menuju masa depan yang lebih cerdas dan efisien.