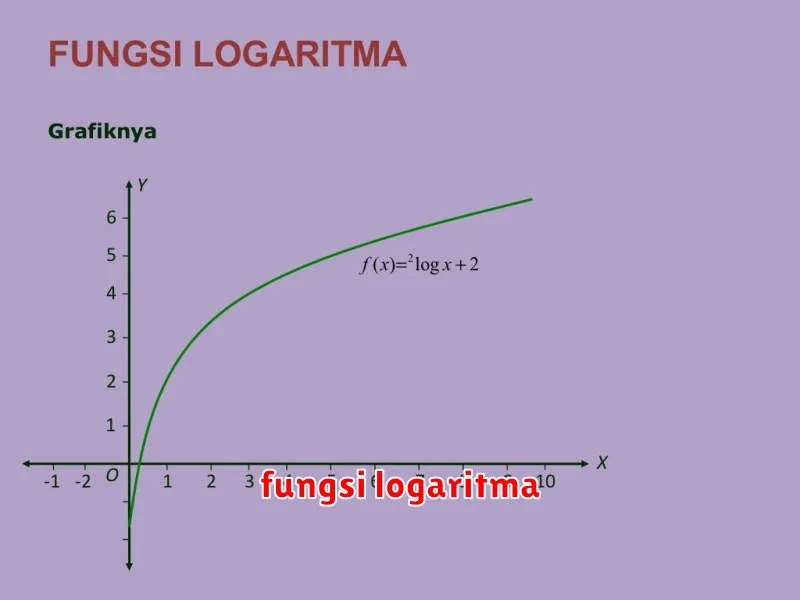
Dalam dunia komputasi yang serba cepat, efisiensi adalah kunci. Setiap kode yang ditulis, setiap algoritma yang dirancang, selalu bertujuan untuk meminimalkan waktu dan sumber daya yang digunakan. Di sinilah peran fungsi logaritma muncul sebagai “pahlawan efisiensi” yang sering kali tersembunyi. Namun jangan salah, di balik kesederhanaan simbol “log” tersimpan kekuatan luar biasa yang dapat memangkas waktu proses komputasi secara signifikan.
Artikel ini akan membawa Anda menyelami lebih dalam dunia fungsi logaritma dan mengungkap bagaimana konsep matematika ini menjadi tulang punggung berbagai aplikasi penting, mulai dari algoritma pencarian hingga kompresi data. Bersiaplah untuk menjelajahi keajaiban logaritma dan temukan bagaimana “log” kecil dapat membuat perbedaan besar dalam dunia komputasi modern.
Memahami Konsep Dasar Logaritma
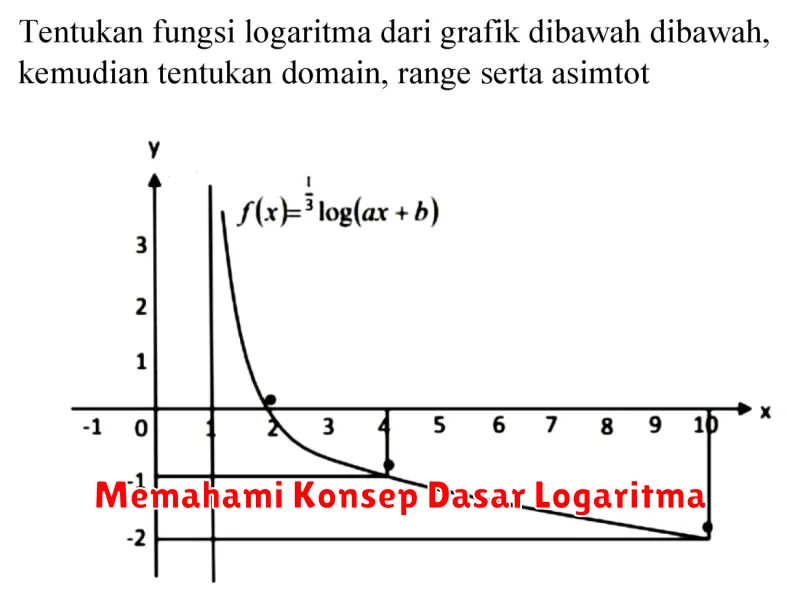
Logaritma seringkali dianggap sebagai salah satu konsep matematika yang menakutkan, namun sebenarnya logaritma cukup mudah dipahami jika kita melihatnya dari sudut pandang yang tepat. Pada dasarnya, logaritma adalah cara lain untuk menyatakan eksponen.
Ingat kembali bahwa eksponen melibatkan basis dan pangkat. Misalnya, dalam 23 = 8, angka 2 adalah basis, 3 adalah pangkat, dan 8 adalah hasil. Logaritma pada dasarnya menanyakan pertanyaan: “Pangkat berapakah yang harus diberikan pada basis tertentu untuk mendapatkan hasil tertentu?”.
Misalnya, logaritma berbasis 2 dari 8 ditulis sebagai log2 8 = 3. Ini berarti “Pangkat berapakah yang harus diberikan pada 2 (basis) untuk mendapatkan 8 (hasil)?”. Jawabannya tentu saja 3.
Secara umum, persamaan logaritma ditulis sebagai:
logb a = c
di mana:
- b adalah basis
- a adalah hasil (atau argument)
- c adalah pangkat
Penting untuk diingat bahwa basis logaritma selalu positif dan tidak sama dengan 1. Ada dua jenis logaritma yang sering digunakan: logaritma basis 10 (log10) yang sering disingkat menjadi “log”, dan logaritma natural (loge) yang disingkat menjadi “ln” dan menggunakan bilangan Euler (e ≈ 2.71828) sebagai basis.
Memahami konsep dasar logaritma sangat penting karena logaritma memiliki banyak aplikasi di berbagai bidang, seperti matematika, sains, komputer, dan teknik. Logaritma digunakan untuk menyederhanakan perhitungan kompleks, memecahkan persamaan eksponensial, memodelkan fenomena dunia nyata seperti pertumbuhan populasi dan peluruhan radioaktif, dan banyak lagi.
Fungsi Logaritma dalam Algoritma dan Struktur Data

Dalam dunia ilmu komputer, terutama dalam ranah algoritma dan struktur data, efisiensi adalah kunci utama. Kita selalu mencari cara untuk membuat program yang berjalan lebih cepat dan menggunakan memori lebih sedikit. Di sinilah peran fungsi logaritma menjadi sangat penting.
Fungsi logaritma, yang sering direpresentasikan sebagai log n, memiliki sifat unik yang membuatnya sangat berharga dalam konteks ini. Tidak seperti fungsi linear (n) atau kuadrat (n2), logaritma tumbuh dengan sangat lambat seiring dengan bertambahnya nilai n. Artinya, untuk nilai n yang sangat besar, nilai log n tetap relatif kecil.
Bagaimana Logaritma Meningkatkan Efisiensi
Bayangkan Anda sedang mencari sebuah nama dalam kamus yang berisi sejuta kata. Jika Anda mencarinya secara linear, dari awal hingga akhir, Anda mungkin perlu memeriksa satu juta kata dalam skenario terburuk. Namun, jika kamus tersebut terurut dan Anda menggunakan metode pencarian biner (binary search), Anda hanya perlu memeriksa sekitar 20 kata. Mengapa? Karena pencarian biner memanfaatkan fungsi logaritma dengan membagi ruang pencarian menjadi dua pada setiap langkahnya.
Contoh lain adalah struktur data seperti pohon biner. Dalam pohon biner seimbang, tinggi pohon (jumlah level) sebanding dengan logaritma dari jumlah node. Ini berarti bahwa operasi seperti pencarian, penyisipan, dan penghapusan node dapat dilakukan dalam waktu O(log n), yang jauh lebih efisien daripada O(n) untuk operasi yang sama dalam struktur data linear seperti array.
Kesimpulan
Fungsi logaritma adalah alat yang sangat kuat dalam pengembangan algoritma dan struktur data. Sifatnya yang tumbuh lambat menjadikannya ideal untuk mengoptimalkan efisiensi program, terutama ketika berhadapan dengan volume data yang besar. Dengan memahami dan memanfaatkan logaritma dengan baik, kita dapat merancang solusi yang lebih cepat, lebih efisien, dan lebih skalabel.
Penerapan Logaritma pada Kompleksitas Waktu

Dalam dunia pengembangan perangkat lunak, efisiensi adalah kunci. Kita menginginkan algoritma yang dapat menyelesaikan tugas dengan cepat dan menggunakan sumber daya seminimal mungkin. Di sinilah kompleksitas waktu berperan, yang membantu kita memahami seberapa baik kinerja suatu algoritma seiring bertambahnya ukuran input.
Salah satu konsep penting dalam kompleksitas waktu adalah logaritma, yang sering direpresentasikan sebagai “log n” dalam notasi Big O. Kompleksitas waktu logaritmik sangat efisien, terutama untuk input berukuran besar. Mengapa? Karena algoritma logaritmik secara efektif “membagi dua” ruang pencarian pada setiap langkah.
Mari kita ambil contoh pencarian biner pada array terurut. Algoritma ini dimulai dengan memeriksa elemen tengah. Jika elemen target lebih kecil, pencarian berlanjut di setengah kiri array. Jika elemen target lebih besar, pencarian berlanjut di setengah kanan. Proses ini berlanjut, dan ruang pencarian terus terbagi dua hingga elemen target ditemukan atau ditentukan tidak ada.
Karena algoritma pencarian biner membagi ruang pencarian menjadi dua pada setiap langkah, ia dapat menemukan elemen target dalam array dengan 1 juta elemen hanya dalam waktu sekitar 20 langkah (log₂1.000.000 ≈ 20). Ini jauh lebih efisien daripada pencarian linear, yang akan membutuhkan waktu hingga 1 juta langkah dalam kasus terburuk.
Penerapan logaritma dalam kompleksitas waktu tidak terbatas pada pencarian biner. Banyak algoritma dan struktur data lain memanfaatkan kekuatan logaritma, seperti:
- Pohon biner: Berbagai operasi pada pohon biner seimbang, seperti penyisipan, penghapusan, dan pencarian, memiliki kompleksitas waktu logaritmik.
- Algoritma rekursif: Algoritma rekursif yang membagi masalah menjadi sub-masalah yang lebih kecil dengan ukuran yang berkurang secara signifikan seringkali menunjukkan kompleksitas waktu logaritmik.
Memahami penerapan logaritma dalam kompleksitas waktu sangat penting bagi pengembang untuk merancang dan memilih algoritma yang efisien dan dapat diskalakan. Dengan memanfaatkan kekuatan logaritma, kita dapat membangun perangkat lunak yang berkinerja baik bahkan dengan jumlah data yang besar.

Dalam dunia pengembangan perangkat lunak, memahami performa dan skalabilitas sebuah aplikasi sangatlah penting. Kita ingin aplikasi kita berjalan cepat dan efisien, bahkan ketika diakses oleh banyak pengguna atau memproses data dalam jumlah besar. Di sinilah logaritma berperan penting dalam analisis performa dan skalabilitas.
Logaritma adalah konsep matematika yang membantu kita memahami pertumbuhan fungsi. Sederhananya, logaritma memberi tahu kita pangkat berapa suatu bilangan dasar harus dipangkatkan untuk mendapatkan bilangan tertentu. Dalam konteks performa, logaritma membantu kita menganalisis kompleksitas waktu dan ruang suatu algoritma.
Mengukur Kompleksitas Waktu
Kompleksitas waktu menggambarkan seberapa cepat waktu eksekusi suatu algoritma meningkat seiring dengan bertambahnya ukuran input. Kita sering menggunakan notasi Big O untuk menyatakan kompleksitas waktu, seperti O(n), O(n log n), atau O(log n).
Algoritma dengan kompleksitas waktu logaritmik (O(log n)) sangat efisien karena waktu eksekusinya tumbuh sangat lambat seiring bertambahnya ukuran input. Contohnya adalah algoritma binary search, yang membagi dua ruang pencarian pada setiap langkahnya. Algoritma ini sangat berguna untuk mencari data dalam struktur data terurut seperti array terurut atau binary tree.
Skalabilitas dan Logaritma
Skalabilitas mengacu pada kemampuan sistem untuk menangani pertumbuhan beban kerja. Aplikasi yang scalable tetap berkinerja baik meskipun terjadi peningkatan jumlah pengguna, data, atau permintaan. Algoritma logaritmik sangat penting untuk membangun aplikasi yang scalable.
Bayangkan sebuah aplikasi web yang perlu mencari informasi dalam database besar. Jika aplikasi menggunakan algoritma pencarian dengan kompleksitas waktu linear (O(n)), waktu respons akan meningkat secara linear seiring dengan pertumbuhan database. Namun, dengan menggunakan algoritma pencarian logaritmik seperti binary search, waktu respons akan tumbuh jauh lebih lambat, memungkinkan aplikasi untuk menangani database yang jauh lebih besar tanpa mengorbankan performa.
Kesimpulan
Logaritma adalah alat penting untuk menganalisis performa dan skalabilitas aplikasi. Memahami kompleksitas waktu algoritma dan memilih algoritma yang tepat, terutama algoritma dengan kompleksitas logaritmik, sangat penting untuk membangun aplikasi yang cepat, efisien, dan scalable. Dengan menguasai konsep logaritma, pengembang dapat membuat aplikasi yang berkinerja tinggi dan mampu menangani pertumbuhan di masa depan.
Studi Kasus: Fungsi Logaritma di Dunia Nyata

Fungsi logaritma, yang seringkali dianggap sebagai konsep matematika yang abstrak, ternyata memiliki peran penting dalam berbagai aspek kehidupan nyata. Dari mengukur kekuatan gempa bumi hingga menghitung tingkat keasaman suatu zat, logaritma membantu kita memahami dan memodelkan fenomena alam dan manusia.
Salah satu contoh penerapan fungsi logaritma yang paling dikenal adalah dalam skala Richter, yang digunakan untuk mengukur kekuatan gempa bumi. Skala ini menggunakan logaritma basis 10 dari amplitudo gelombang seismik yang terekam oleh seismograf. Artinya, setiap kenaikan satu tingkat pada skala Richter mewakili peningkatan sepuluh kali lipat dalam amplitudo gelombang gempa. Dengan kata lain, gempa bumi dengan magnitudo 7 pada skala Richter memiliki amplitudo gelombang 10 kali lebih besar daripada gempa bumi dengan magnitudo 6.
Selain seismologi, logaritma juga berperan penting dalam bidang kimia. Skala pH, yang mengukur tingkat keasaman atau kebasaan suatu larutan, juga menggunakan logaritma. Skala pH didefinisikan sebagai logaritma negatif dari konsentrasi ion hidrogen (H+) dalam suatu larutan. Semakin rendah nilai pH, semakin asam larutan tersebut. Skala pH memiliki rentang dari 0 hingga 14, dengan 7 menunjukkan larutan netral. Larutan dengan pH kurang dari 7 bersifat asam, sedangkan larutan dengan pH lebih dari 7 bersifat basa.
Di bidang musik, logaritma digunakan untuk memahami interval nada dan tangga nada. Misalnya, rasio frekuensi antara dua nada yang berjarak satu oktaf adalah 2:1. Dengan menggunakan logaritma, kita dapat membagi oktaf menjadi 12 bagian yang sama, yang dikenal sebagai setengah nada. Sistem pembagian nada ini memungkinkan terciptanya sistem musik yang harmonis dan mudah dipahami.
Contoh-contoh di atas hanyalah sebagian kecil dari banyaknya aplikasi fungsi logaritma dalam kehidupan sehari-hari. Dari ilmu pengetahuan hingga seni, logaritma membantu kita memahami dan menavigasi dunia di sekitar kita. Pemahaman tentang logaritma memungkinkan kita untuk mengukur dan memodelkan fenomena kompleks dengan cara yang lebih sederhana dan mudah dipahami.