Pernahkah Anda membayangkan bagaimana musik favorit Anda dapat tersimpan dalam sebuah file digital, atau bagaimana gambar menakjubkan dapat dikirimkan melalui internet dalam sekejap mata? Jawabannya terletak pada kekuatan magis sinyal digital dan transformasi matematika yang luar biasa yang dikenal sebagai Transformasi Fourier.
Dalam artikel ini, kita akan memulai petualangan seru untuk mengungkap misteri di balik sinyal digital dan memahami bagaimana Transformasi Fourier menjadi kunci dalam merevolusi dunia kita. Bersiaplah untuk menyelami dunia di mana gelombang suara dan cahaya diubah menjadi angka-angka ajaib, membuka jalan bagi keajaiban teknologi modern seperti internet, ponsel pintar, dan banyak lagi!
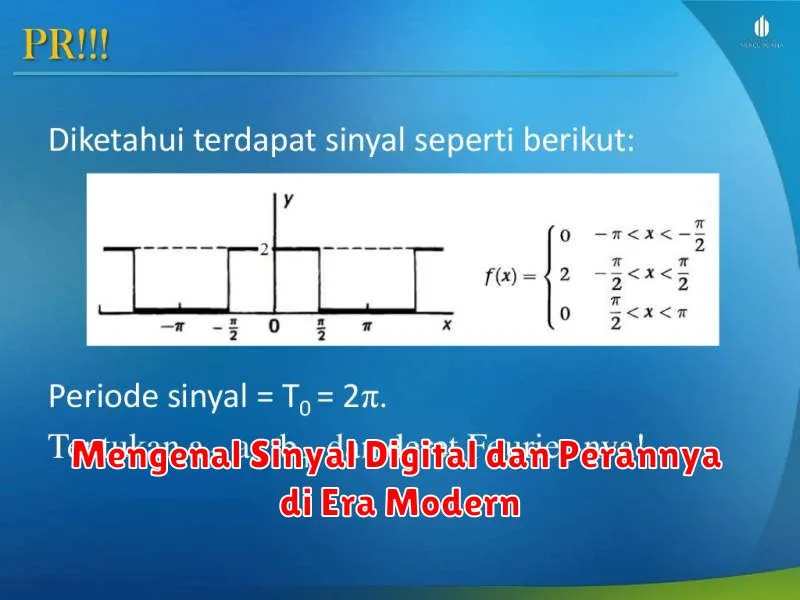
Mengenal Sinyal Digital dan Perannya di Era Modern
Di era modern yang serba canggih ini, kita dikelilingi oleh berbagai teknologi yang mengandalkan sinyal digital. Dari smartphone yang kita gunakan untuk berkomunikasi, komputer yang kita pakai untuk bekerja, hingga internet yang menghubungkan kita dengan seluruh dunia, semuanya bergantung pada kemampuan sinyal digital untuk mengirimkan informasi secara cepat dan akurat.
Tapi sebenarnya, apa itu sinyal digital? Secara sederhana, sinyal digital adalah jenis sinyal yang merepresentasikan informasi dalam bentuk angka atau digit. Berbeda dengan sinyal analog yang merepresentasikan informasi dalam bentuk gelombang kontinu, sinyal digital menggunakan serangkaian nilai diskrit (biasanya 0 dan 1) untuk mewakili data.
Keuntungan utama dari sinyal digital adalah kemampuannya dalam mengirimkan informasi dengan akurasi tinggi dan tahan terhadap gangguan. Karena data direpresentasikan dalam bentuk angka, maka kecil kemungkinannya terjadi kesalahan interpretasi saat sinyal ditransmisikan melalui media seperti kabel atau gelombang radio. Selain itu, sinyal digital juga lebih mudah diproses, disimpan, dan dimanipulasi menggunakan komputer.
Peran Sinyal Digital di Berbagai Bidang
Sinyal digital memainkan peran yang sangat penting dalam berbagai bidang, antara lain:
- Komunikasi: Telepon seluler, internet, televisi digital, dan radio digital semuanya menggunakan sinyal digital untuk mengirimkan suara, gambar, dan data.
- Komputer: Semua jenis komputer, dari laptop hingga superkomputer, menggunakan sinyal digital untuk memproses dan menyimpan informasi.
- Elektronik Konsumen: Peralatan elektronik seperti televisi, pemutar musik, kamera digital, dan konsol game semuanya menggunakan sinyal digital.
- Kedokteran: Sinyal digital digunakan dalam berbagai peralatan medis, seperti mesin MRI, CT scan, dan monitor jantung, untuk menghasilkan gambar dan data medis.
- Industri: Sistem kontrol otomatis di pabrik dan proses industri lainnya sangat bergantung pada sinyal digital.
Masa Depan Sinyal Digital
Di masa depan, peran sinyal digital diprediksi akan semakin besar seiring dengan perkembangan teknologi seperti Internet of Things (IoT), kecerdasan buatan (AI), dan komputasi awan. Dengan kemampuannya dalam mengirimkan informasi secara cepat, akurat, dan efisien, sinyal digital akan terus menjadi tulang punggung bagi perkembangan teknologi di masa depan.
Transformasi Fourier: Jendela Menuju Frekuensi Tersembunyi

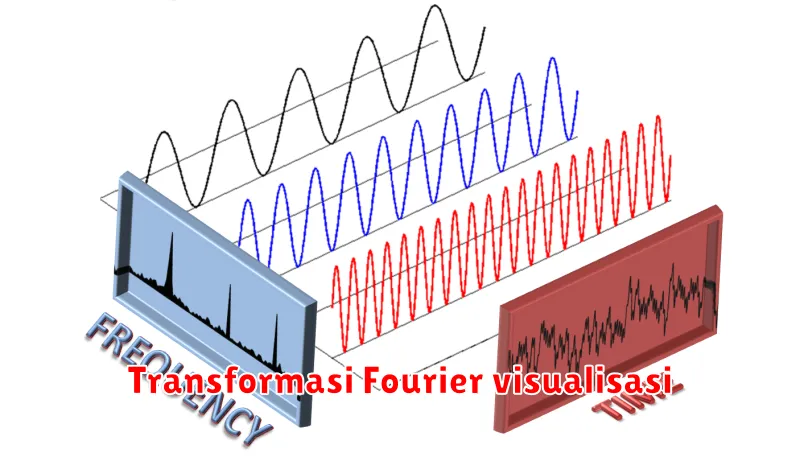
Di dunia yang dipenuhi sinyal dan gelombang, bagaimana kita mengungkap rahasia tersembunyi di balik data yang kompleks? Jawabannya terletak pada alat matematika yang kuat yang dikenal sebagai Transformasi Fourier. Bayangkan sebuah prisma yang memisahkan cahaya putih menjadi spektrum warna-warni. Demikian pula, Transformasi Fourier memungkinkan kita untuk menguraikan sinyal yang kompleks menjadi komponen frekuensi individualnya.
Konsep dasar di balik Transformasi Fourier adalah bahwa setiap sinyal periodik, betapapun rumitnya, dapat direpresentasikan sebagai jumlah dari gelombang sinus dan kosinus dengan frekuensi, amplitudo, dan fase yang berbeda. Proses ini seperti membongkar sebuah akord musik menjadi nada-nada penyusunnya. Dengan menganalisis frekuensi-frekuensi ini, kita dapat memperoleh wawasan berharga tentang sifat dan karakteristik sinyal asli.
Aplikasi Transformasi Fourier
Transformasi Fourier memiliki aplikasi yang luas di berbagai bidang, antara lain:
- Pengolahan Sinyal: Untuk menganalisis sinyal audio, gambar, dan video, menghilangkan noise, dan melakukan kompresi data.
- Telekomunikasi: Untuk memodulasi dan mendemodulasi sinyal, memungkinkan transmisi data nirkabel yang efisien.
- Pengolahan Gambar Medis: Untuk meningkatkan kualitas gambar medis, seperti sinar-X dan MRI, dan mengekstrak informasi diagnostik.
- Kimia dan Fisika: Untuk mempelajari struktur molekul, menganalisis spektrum cahaya, dan memodelkan fenomena fisika.
Kesimpulan
Transformasi Fourier adalah alat yang sangat berharga untuk memahami dan memanipulasi sinyal di dunia modern. Dengan kemampuannya untuk mengungkap frekuensi tersembunyi dalam data, Transformasi Fourier telah merevolusi banyak bidang dan terus memainkan peran penting dalam kemajuan teknologi dan ilmiah.
Memecah Belah Sinyal: Mengurai Komponen Frekuensi

Di dunia yang dipenuhi gelombang dan sinyal, memahami konsep frekuensi sangatlah penting. Bayangkan sebuah orkestra yang memainkan simfoni yang kompleks. Setiap alat musik menghasilkan suara dengan frekuensi yang berbeda, dan kombinasi dari semua frekuensi ini menciptakan musik yang indah.
Sinyal, seperti gelombang suara atau gelombang elektromagnetik, juga merupakan kombinasi dari berbagai frekuensi. Dengan “memecah” sinyal menjadi komponen frekuensinya, kita dapat menganalisis dan memanipulasinya dengan cara yang luar biasa. Proses ini seperti memisahkan cahaya putih menjadi warna-warna pelangi menggunakan prisma.
Salah satu alat yang paling penting dalam analisis frekuensi adalah Transformasi Fourier. Dinamai dari matematikawan dan fisikawan Prancis Joseph Fourier, teknik matematika ini menguraikan sinyal menjadi sejumlah gelombang sinus dan kosinus dengan frekuensi yang berbeda. Amplitudo setiap gelombang sinus atau kosinus menunjukkan seberapa besar kontribusi frekuensi tersebut terhadap sinyal keseluruhan.
Analisis frekuensi memiliki aplikasi yang luas di berbagai bidang. Dalam pengolahan sinyal audio, misalnya, digunakan untuk mengidentifikasi dan memanipulasi frekuensi yang berbeda dalam musik, ucapan, atau suara lainnya. Ini memungkinkan kita untuk melakukan tugas-tugas seperti menghilangkan noise, menyamakan audio, dan mengenali ucapan.
Di bidang telekomunikasi, analisis frekuensi sangat penting untuk mentransmisikan informasi melalui gelombang radio. Dengan memodulasi sinyal informasi ke frekuensi pembawa yang berbeda, beberapa sinyal dapat berbagi media transmisi yang sama tanpa saling mengganggu. Ini adalah prinsip di balik radio, televisi, dan komunikasi seluler.
Analisis frekuensi juga memainkan peran penting dalam pengolahan citra. Dengan menganalisis frekuensi spasial dalam gambar, kita dapat melakukan tugas-tugas seperti menajamkan tepi, menghilangkan blur, dan mendeteksi pola.
Singkatnya, memahami dan memanipulasi komponen frekuensi sinyal membuka dunia kemungkinan di berbagai bidang. Dari musik hingga telekomunikasi hingga pengolahan citra, analisis frekuensi adalah alat yang ampuh yang memungkinkan kita untuk mengekstrak informasi dan memanipulasi sinyal dengan cara yang luar biasa.
Aplikasi Konkret: Dari Analisis Suara Hingga Pengolahan Citra
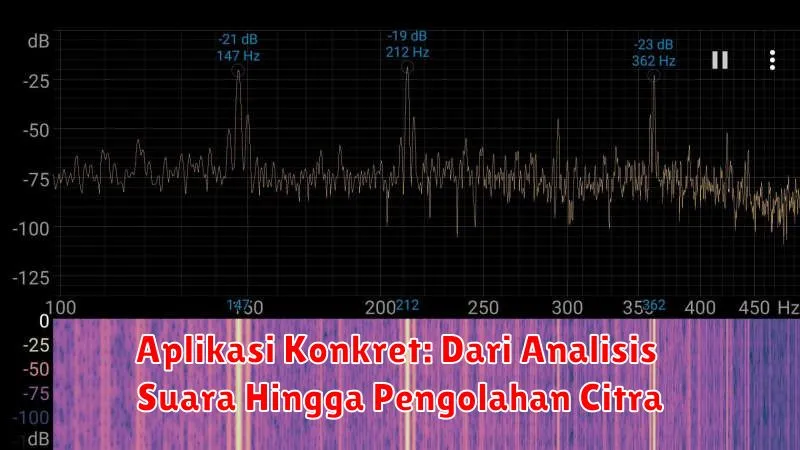
Dunka teknologi terus berkembang dengan pesat, dan salah satu bidang yang mengalami kemajuan signifikan adalah kecerdasan buatan (Artificial Intelligence/AI). Tidak hanya menjadi topik hangat di kalangan akademisi dan peneliti, AI kini telah merambah ke berbagai aspek kehidupan kita, menawarkan solusi inovatif untuk berbagai masalah kompleks.
Salah satu contoh nyata dari aplikasi AI adalah dalam bidang analisis suara. Teknologi pengenalan suara, seperti yang digunakan pada asisten virtual seperti Siri dan Alexa, telah merevolusi cara kita berinteraksi dengan perangkat elektronik. Lebih dari sekadar perintah suara sederhana, analisis suara kini dapat digunakan untuk mendeteksi emosi, mengidentifikasi penutur, dan bahkan mendiagnosis kondisi medis berdasarkan suara batuk atau pola bicara.
Di bidang pengolahan citra, AI juga menunjukkan kemampuannya yang luar biasa. Algoritma AI dapat dilatih untuk “melihat” dan menginterpretasi gambar dengan akurasi yang mengesankan. Teknologi ini mendasari berbagai aplikasi, mulai dari mobil self-driving yang dapat mengenali objek di sekitarnya, hingga alat diagnosa medis yang dapat mendeteksi tumor dan kelainan lainnya pada gambar medis.
Tentu saja, potensi AI jauh melampaui contoh-contoh di atas. Dari sektor keuangan hingga pertanian, AI memiliki potensi untuk meningkatkan efisiensi, produktivitas, dan bahkan membantu kita dalam memecahkan beberapa tantangan global yang paling mendesak.
Meskipun masih banyak yang harus dijelajahi, satu hal yang pasti: AI akan terus memainkan peran yang semakin penting dalam membentuk masa depan kita. Memahami potensi dan aplikasi konkretnya adalah kunci untuk memanfaatkan kekuatan transformatif teknologi ini.
Keunggulan Transformasi Fourier dalam Pengolahan Sinyal Digital

Transformasi Fourier adalah alat yang sangat penting dalam pengolahan sinyal digital. Ia memungkinkan kita untuk menganalisis sinyal dari domain waktu ke domain frekuensi. Mengapa ini penting? Karena banyak informasi tersembunyi dalam representasi frekuensi sinyal, yang tidak mudah dilihat dalam domain waktu.
Salah satu keunggulan utama Transformasi Fourier adalah kemampuannya untuk mengurai sinyal kompleks menjadi komponen-komponen frekuensi penyusunnya. Bayangkan sebuah orkestra yang memainkan musik yang rumit. Dengan Transformasi Fourier, kita dapat mengidentifikasi frekuensi setiap alat musik yang dimainkan, meskipun semua alat musik tersebut dimainkan bersamaan. Hal ini memungkinkan kita untuk menganalisis kontribusi setiap instrumen terhadap suara keseluruhan.
Keunggulan lainnya adalah kemampuannya dalam mendeteksi pola tersembunyi. Dalam domain waktu, pola-pola tertentu mungkin sulit dikenali karena tersembunyi oleh noise atau variasi acak. Namun, dalam domain frekuensi, pola-pola ini seringkali muncul sebagai puncak yang jelas. Sebagai contoh, dalam pemrosesan gambar medis, Transformasi Fourier dapat membantu mendeteksi tumor atau anomali lainnya yang tidak terlihat dengan jelas dalam gambar asli.
Transformasi Fourier juga memungkinkan kita untuk melakukan pemrosesan sinyal yang efisien. Banyak operasi pemrosesan sinyal, seperti filtering dan kompresi, lebih mudah dan efisien dilakukan dalam domain frekuensi. Setelah pemrosesan selesai, sinyal dapat diubah kembali ke domain waktu menggunakan Transformasi Fourier Invers.
Secara keseluruhan, Transformasi Fourier adalah alat yang sangat berharga dalam pengolahan sinyal digital. Kemampuannya untuk menganalisis sinyal dalam domain frekuensi membuka berbagai kemungkinan untuk pemrosesan, analisis, dan manipulasi sinyal, yang mengarah pada kemajuan di berbagai bidang seperti telekomunikasi, audio, video, dan pemrosesan gambar.