Di era digital yang dipenuhi data ini, kemampuan untuk mengolah dan memahami informasi menjadi kunci kesuksesan di berbagai bidang. Namun, bagaimana jika kita dapat melangkah lebih jauh dari sekadar memahami data? Bagaimana jika kita dapat mengungkap pola tersembunyi, memprediksi tren masa depan, dan membuat keputusan yang lebih tepat? Di sinilah kekuatan kalkulus integral berperan.
Lebih dari sekadar rumus matematika yang rumit, kalkulus integral adalah alat canggih yang memungkinkan kita untuk menganalisis data dengan tingkat presisi dan kedalaman yang belum pernah terjadi sebelumnya. Dalam artikel ini, kita akan menguak bagaimana kalkulus integral dapat membantu kita dalam menganalisis data secara lebih tajam dan akurat, membuka pintu menuju pemahaman yang lebih baik dan pengambilan keputusan yang lebih cerdas.
Memahami Konsep Dasar Kalkulus Integral

Kalkulus, dengan cabang-cabangnya yang luas seperti kalkulus diferensial dan integral, seringkali dianggap sebagai momok bagi banyak pelajar. Namun, di balik rumus dan simbol yang kompleks, tersimpan konsep-konsep yang sebenarnya mudah dipahami jika dijelaskan dengan tepat.
Dalam artikel ini, kita akan menyelami dunia kalkulus integral, memahami inti sari dari konsep dasarnya, dan melihat bagaimana penerapannya dalam kehidupan sehari-hari.
Apa Itu Kalkulus Integral?
Sederhananya, kalkulus integral adalah kebalikan dari kalkulus diferensial. Jika diferensial berfokus pada pencarian laju perubahan sesaat, integral justru mencari tahu akumulasi perubahan total dari suatu fungsi.
Bayangkan Anda memiliki grafik kecepatan mobil terhadap waktu. Kalkulus diferensial membantu kita menentukan percepatan mobil pada suatu titik waktu tertentu. Di sisi lain, kalkulus integral memungkinkan kita menghitung jarak total yang ditempuh mobil dalam selang waktu tertentu.
Konsep Dasar Kalkulus Integral
Konsep dasar kalkulus integral terletak pada pemahaman tentang integral tentu dan integral tak tentu.
- Integral Tak Tentu: Merupakan operasi kebalikan dari turunan. Jika F'(x) = f(x), maka integral tak tentu dari f(x) adalah F(x) + C, di mana C adalah konstanta integrasi.
- Integral Tentu: Digunakan untuk menghitung nilai pasti dari suatu integral pada selang tertentu. Integral tentu dilambangkan dengan simbol integral dengan batas atas dan batas bawah.
Penerapan Kalkulus Integral dalam Kehidupan Sehari-hari
Meskipun terkesan abstrak, kalkulus integral memiliki banyak aplikasi praktis di berbagai bidang, seperti:
- Fisika: Menghitung kerja yang dilakukan oleh gaya, menentukan pusat massa, dan menganalisis gerak benda.
- Ekonomi: Memprediksi pertumbuhan ekonomi, menganalisis kurva permintaan dan penawaran, dan mengoptimalkan keuntungan.
- Statistika: Menghitung probabilitas, menentukan nilai harapan, dan menganalisis distribusi data.
Kesimpulan
Kalkulus integral adalah alat matematika yang sangat powerful dengan aplikasi yang luas dalam berbagai disiplin ilmu. Memahami konsep dasarnya membuka pintu bagi kita untuk memahami dunia di sekitar kita dengan lebih baik.
Aplikasi Kalkulus Integral dalam Analisis Data

Kalkulus integral, seringkali dianggap sebagai konsep matematika yang abstrak, sebenarnya memiliki aplikasi yang luas dan signifikan dalam berbagai bidang, termasuk analisis data. Meskipun sekilas tampak tidak berhubungan, kalkulus integral menyediakan perangkat yang ampuh untuk mengekstrak informasi berharga dari data dan memahami tren yang mendasarinya.
Salah satu aplikasi utama kalkulus integral dalam analisis data adalah dalam menghitung luas di bawah kurva. Dalam konteks ini, kurva sering kali mewakili distribusi probabilitas dari suatu variabel. Dengan menghitung luas di bawah kurva dalam rentang tertentu, kita dapat menentukan probabilitas suatu nilai berada dalam rentang tersebut. Konsep ini sangat penting dalam statistika dan pembelajaran mesin, di mana pemahaman distribusi data sangat penting untuk pengambilan keputusan dan prediksi yang akurat.
Selain itu, kalkulus integral juga berperan penting dalam menghitung nilai rata-rata atau nilai ekspektasi dari suatu fungsi. Dalam analisis data, fungsi ini bisa merepresentasikan berbagai hal, seperti biaya produksi, pendapatan penjualan, atau jumlah pengguna aktif dalam suatu platform. Dengan menghitung integral fungsi tersebut terhadap distribusi probabilitas yang relevan, kita dapat memperoleh nilai ekspektasi yang memberikan gambaran umum tentang perilaku variabel tersebut.
Lebih lanjut, kalkulus integral menjadi dasar bagi banyak algoritma pembelajaran mesin. Contohnya, algoritma gradient descent, yang digunakan untuk melatih model pembelajaran mesin, bergantung pada turunan (kebalikan dari integral) untuk menemukan nilai optimal dari parameter model. Dengan memahami kalkulus integral, kita dapat memahami cara kerja algoritma ini secara lebih mendalam dan bahkan mengembangkan algoritma baru yang lebih efisien.
Meskipun mungkin tidak selalu terlihat jelas, kalkulus integral memainkan peran penting di balik layar dalam banyak teknik analisis data yang kita gunakan saat ini. Memahami konsep dasar kalkulus integral dapat memberikan apresiasi yang lebih dalam tentang bagaimana data dianalisis dan bagaimana informasi berharga diekstraksi dari data mentah. Dengan demikian, mempelajari kalkulus integral dapat menjadi investasi yang berharga bagi siapa pun yang ingin mendalami dunia analisis data.
Menghitung Luas di Bawah Kurva untuk Menemukan Probabilitas
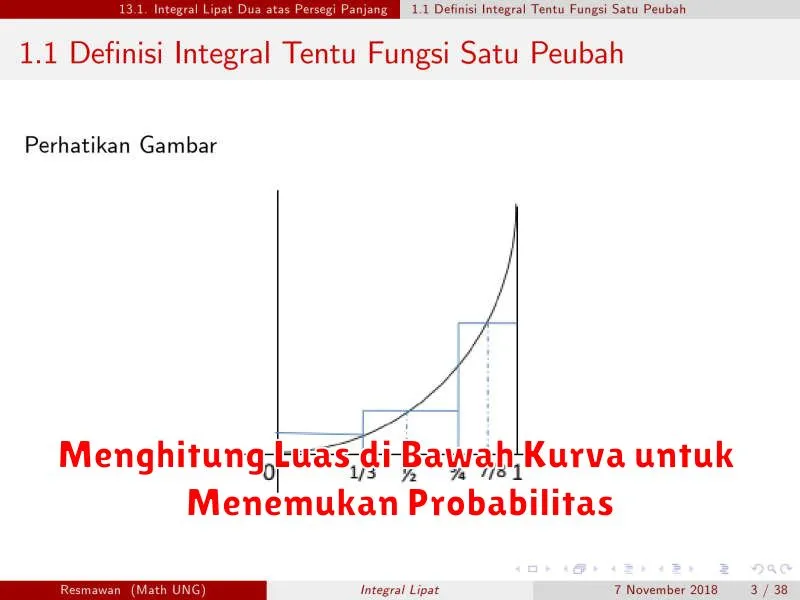
Dalam statistika dan probabilitas, kita sering berhadapan dengan distribusi probabilitas kontinu, yang digambarkan dalam bentuk kurva. Luas di bawah kurva ini memiliki makna yang penting: ia merepresentasikan probabilitas dari suatu rentang nilai yang mungkin untuk variabel acak.
Misalnya, jika kita memiliki distribusi normal standar, luas di bawah kurva antara z-score -1 dan 1 adalah sekitar 68%. Artinya, terdapat probabilitas 68% bahwa nilai variabel acak yang mengikuti distribusi tersebut akan jatuh antara -1 dan 1 standar deviasi dari mean.
Menghitung Luas di Bawah Kurva
Menghitung luas di bawah kurva secara manual bisa rumit, terutama untuk distribusi yang kompleks. Untungnya, terdapat beberapa cara untuk melakukannya:
- Menggunakan Tabel Distribusi: Tabel ini menyediakan luas di bawah kurva untuk nilai-nilai tertentu. Kita dapat mencari luas yang sesuai dengan rentang nilai yang kita inginkan.
- Menggunakan Kalkulator Ilmiah: Banyak kalkulator ilmiah memiliki fungsi untuk menghitung luas di bawah kurva untuk distribusi umum seperti distribusi normal.
- Menggunakan Software Statistik: Software seperti R, Python (dengan library seperti SciPy), atau SPSS dapat menghitung luas di bawah kurva dengan akurat dan efisien.
Penerapan Menghitung Luas di Bawah Kurva
Konsep menghitung luas di bawah kurva memiliki banyak aplikasi di berbagai bidang:
- Pengujian Hipotesis: Menentukan probabilitas mendapatkan hasil pengamatan tertentu jika hipotesis nol benar.
- Interval Kepercayaan: Memperkirakan rentang nilai yang mungkin untuk parameter populasi.
- Analisis Risiko: Menghitung probabilitas suatu peristiwa yang tidak diinginkan terjadi.
Dengan memahami hubungan antara luas di bawah kurva dan probabilitas, kita dapat menginterpretasikan data dan menarik kesimpulan yang lebih bermakna dalam berbagai konteks.
Menentukan Volume Objek Kompleks dalam Visualisasi Data

Dalam dunia visualisasi data, kita sering dihadapkan pada kebutuhan untuk memahami dan menganalisis objek tiga dimensi yang kompleks. Salah satu parameter penting yang membantu kita dalam hal ini adalah volume.
Menghitung volume objek sederhana seperti kubus atau bola relatif mudah dengan rumus matematika. Namun, bagaimana jika kita berhadapan dengan objek yang bentuknya tidak beraturan atau memiliki permukaan yang kompleks? Di sinilah peran visualisasi data dan perangkat lunak analisis menjadi sangat penting.
Dengan bantuan teknologi modern, kita dapat membuat representasi visual dari data tiga dimensi yang rumit. Perangkat lunak visualisasi memungkinkan kita untuk “memotong” objek secara virtual, melihatnya dari berbagai sudut pandang, dan bahkan menghitung volume secara akurat meskipun bentuknya tidak beraturan.
Proses ini umumnya melibatkan langkah-langkah berikut:
- Akuisisi Data: Data 3D objek diperoleh melalui pemindaian, pemodelan, atau sumber lainnya.
- Pemrosesan Data: Data mentah dibersihkan, dirapikan, dan diubah menjadi format yang sesuai untuk visualisasi.
- Rekonstruksi Permukaan: Permukaan objek direkonstruksi dari data titik atau jala poligon.
- Perhitungan Volume: Algoritma khusus digunakan untuk menghitung volume objek berdasarkan permukaan yang telah direkonstruksi.
Kemampuan untuk menentukan volume objek kompleks dalam visualisasi data memiliki banyak aplikasi praktis, antara lain:
- Geologi dan Eksplorasi Sumber Daya: Menentukan volume cadangan mineral di bawah tanah.
- Kedokteran dan Kesehatan: Menganalisis volume tumor atau organ dalam tubuh pasien.
- Manufaktur dan Desain: Menghitung kebutuhan material dan optimalisasi desain produk.
Dengan demikian, kemampuan untuk menentukan volume objek kompleks dalam visualisasi data membuka peluang baru untuk pemahaman yang lebih dalam dan pengambilan keputusan yang lebih tepat di berbagai bidang.
Mengukur Laju Perubahan Data dari Waktu ke Waktu

Dalam dunia yang terus berubah ini, data menjadi aset yang sangat berharga. Namun, data yang statis tidaklah cukup. Kita perlu memahami bagaimana data berubah dari waktu ke waktu untuk dapat membuat keputusan yang tepat. Di sinilah pentingnya mengukur laju perubahan data.
Laju perubahan data menunjukkan seberapa cepat suatu variabel berubah dalam periode waktu tertentu. Informasi ini sangat penting dalam berbagai bidang, seperti:
- Bisnis: Memantau pertumbuhan penjualan, perubahan pangsa pasar, dan tren konsumen.
- Keuangan: Menganalisis pergerakan harga saham, fluktuasi nilai tukar, dan indikator ekonomi lainnya.
- Kesehatan: Melacak penyebaran penyakit, efektivitas pengobatan, dan tren kesehatan masyarakat.
Terdapat beberapa metode yang dapat digunakan untuk mengukur laju perubahan data, antara lain:
1. Persentase Perubahan
Metode ini menghitung selisih antara dua titik data dan membaginya dengan nilai awal. Hasilnya kemudian dikalikan dengan 100% untuk mendapatkan persentase perubahan. Rumusnya adalah:
(Nilai Akhir - Nilai Awal) / Nilai Awal x 100%
2. Laju Pertumbuhan Tahunan Gabungan (CAGR)
CAGR mengukur laju pertumbuhan rata-rata per tahun selama periode waktu tertentu, dengan asumsi pertumbuhan terjadi secara eksponensial. Rumusnya adalah:
((Nilai Akhir / Nilai Awal)^(1 / Jumlah Tahun) - 1) x 100%
3. Analisis Regresi
Metode ini digunakan untuk menemukan hubungan matematis antara variabel dependen (data yang ingin diukur) dan variabel independen (waktu). Dengan analisis regresi, kita dapat memprediksi nilai data di masa depan berdasarkan tren historis.
Memilih metode yang tepat tergantung pada jenis data dan tujuan analisis. Penting untuk memahami kelebihan dan kekurangan setiap metode sebelum mengaplikasikannya.
Dengan memahami laju perubahan data, kita dapat:
- Mengidentifikasi tren dan pola.
- Membuat prediksi yang lebih akurat.
- Mengambil keputusan yang lebih tepat dan efektif.
Dalam era data yang terus berkembang, kemampuan untuk mengukur dan menginterpretasikan laju perubahan data menjadi semakin penting. Dengan memanfaatkan alat dan teknik yang tepat, kita dapat mengubah data menjadi informasi yang berharga dan meningkatkan pengambilan keputusan di berbagai bidang.
Memprediksi Tren Masa Depan dengan Ekstrapolasi
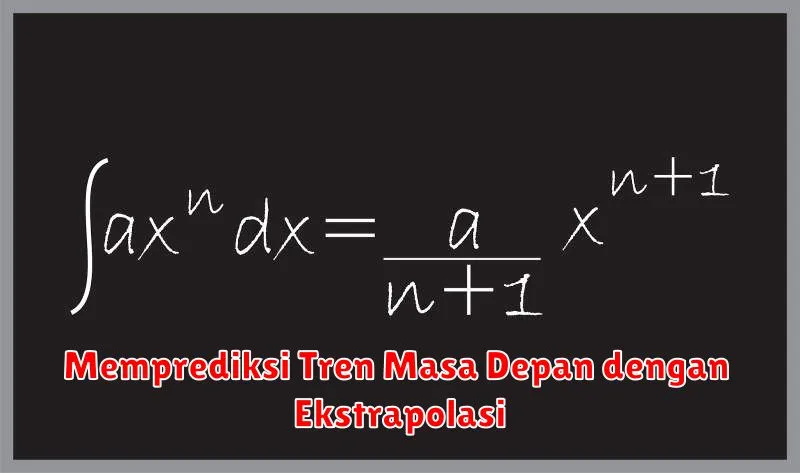
Di dunia yang terus berubah ini, kemampuan untuk memprediksi tren masa depan menjadi semakin penting. Salah satu metode yang sering digunakan adalah ekstrapolasi. Sederhananya, ekstrapolasi adalah proses memperkirakan nilai di luar rentang data yang diketahui dengan memperpanjang tren yang ada.
Bayangkan Anda sedang melacak penjualan produk selama beberapa bulan terakhir. Data menunjukkan tren peningkatan yang stabil. Dengan ekstrapolasi, Anda dapat memperkirakan penjualan di bulan-bulan mendatang dengan mengasumsikan tren tersebut akan berlanjut. Tentu saja, ini hanyalah prediksi dan akurasinya bergantung pada berbagai faktor.
Faktor yang Mempengaruhi Akurasi Ekstrapolasi
Penting untuk diingat bahwa ekstrapolasi bukanlah ilmu pasti. Ada beberapa faktor yang dapat memengaruhi akurasinya, antara lain:
- Kualitas Data: Data yang akurat dan andal sangat penting untuk ekstrapolasi yang akurat.
- Panjang Data: Semakin panjang rentang data yang tersedia, semakin baik dasar untuk ekstrapolasi.
- Faktor Eksternal: Peristiwa tak terduga, seperti perubahan ekonomi atau bencana alam, dapat memengaruhi tren masa depan.
Keuntungan dan Kerugian Ekstrapolasi
Seperti metode prediksi lainnya, ekstrapolasi memiliki kelebihan dan kekurangan. Berikut adalah beberapa di antaranya:
Keuntungan:
- Sederhana dan Mudah Digunakan: Ekstrapolasi relatif mudah dipahami dan diterapkan.
- Berguna untuk Tren Jangka Pendek: Dalam kondisi yang stabil, ekstrapolasi dapat memberikan perkiraan yang masuk akal untuk jangka pendek.
Kerugian:
- Rentan terhadap Kesalahan: Ekstrapolasi mengasumsikan tren akan berlanjut, yang mungkin tidak selalu terjadi.
- Tidak Memperhitungkan Faktor Eksternal: Ekstrapolasi tidak dapat memprediksi peristiwa tak terduga yang dapat memengaruhi tren.
Kesimpulan
Ekstrapolasi dapat menjadi alat yang berguna untuk memprediksi tren masa depan, tetapi penting untuk menggunakannya dengan hati-hati. Pahami batasannya dan pertimbangkan faktor-faktor yang dapat memengaruhi keakuratannya. Ingatlah bahwa ekstrapolasi hanyalah prediksi dan bukan jaminan.




